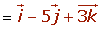UNIDAD
#1
NATURALEZA DE LA FÍSICA
El vocablo física procede del griego y significa el
conocimiento del mundo natural. Por lo tanto, no nos ha de sorprender que los
primeros esfuerzos registrados por el ser humano para reunir sistemáticamente
el conocimiento sobre el movimiento de los cuerpos procedan de la antigua
Grecia. En la filosofía natural establecida por Aristóteles (384–322 a.C.), las
explicaciones de los fenómenos físicos se deducían de hipótesis sobre el mundo
y no de la experimentación.
Es la Ciencia que se encarga de estudiar los fenómenos
naturales, en los cuales no hay cambios en la composición de la materia.
La Física ha experimentado un gran desarrollo gracias al
esfuerzo de notables científicos e investigadores, quienes al inventar y
perfeccionar instrumentos, aparatos y equipos han logrado que el hombre agudice
sus sentidos al detectar, observar y analizar fenómenos.
Por ejemplo, cuando se escribe L=1500 m, que se
lee "ele igual a mil quinientos metros" se quiere decir que la longitud
denominada L mide aproximadamente 1500 veces más que la longitud del
metro patrón, que es lo mismo que decir L=1,5 km (por convenio, no se
consideran cifras significativas los ceros finales, excepto si son cifras
decimales), y que no tiene sentido si sólo se dice "L=1,5".
Incluso si toda la Humanidad llegase a usar exclusivamente un único sistema de
unidades sin múltiplos ni submúltiplos, se seguiría indicando la unidad patrón
para reconocer el tipo de magnitud física involucrada.
El Sistema Internacional (SI) de Unidades fue establecido a mediados del siglo XX como
medio para unificar las unidades de medida en todo el mundo, para lo cual tomó
como base el sistema métrico decimal. Este sistema se ha extendido en la
norma ISO 80000 para formar el Sistema Internacional de Magnitudes, que
además incluye símbolos de magnitudes y aclaraciones adicionales.
A cada unidad le corresponde un símbolo y un nombre. Según el
SI, el símbolo no es una abreviatura del nombre de la unidad, sino que es una entidad
matemática con valor propio: el símbolo representa una determinada cantidad de
la magnitud que se mide, de modo que 3 kg es el triple de la cantidad
representada por kg (la masa de una pieza que sirve como patrón) y que como tal
se puede operar.
IMPORTANCIA.- La Física es importante
porque es una de las ciencias naturales que más ha contribuido al desarrollo y
bienestar del hombre, porque gracias a su estudio e investigación ha sido
posible encontrar en muchos casos, una explicación clara y útil a los fenómenos
que se presentan en nuestra vida diaria.
SÍMBOLOS DE LAS
UNIDADES
Los patrones básicos se llaman unidades de medida. Para
especificar el valor de una magnitud hay que dar la unidad de medida y el
número que relaciona ambos valores. De nada sirve decir que la altura de un
árbol es de 5 veces no sé qué, que decir que es de no sé cuántos metros. Aunque
la relación del valor numérico con la unidad de medida es multiplicativa (p.e.
5 veces un metro), la norma de escritura es separar con un espacio en blanco
ambos términos.
Además los símbolos de las unidades tienen reglas que son:
v Los símbolos de las unidades nunca
llevan punto final y no tienen plural.
v Cuando se usan prefijos el símbolo de
la unidad se escribe después del prefijo y sin espacio entre ambos.
v Los símbolos de las unidades se
derivan de nombres propios que se escriben con la letra inicial mayúscula, los
demás símbolos se escriben con letras minúsculas.
v Para expresar un producto de símbolos
de las unidades se usa un punto en la mitad de las unidades. El punto se puede
suprimir si existe la posibilidad de confusión.
v Cuando una unidad es derivada o
secundaria, se forma dividiendo una unidad para otra. Se puede escribir por
ejemplo, m/s o equivalente m*s-1.
SISTEMA DE MEDICIÓN DE
UNIDADES
Existen tres mediciones y son:
·
Básicas
·
Derivadas
·
Suplementarias
BÁSICAS
UNIDADES Y CONVERSIONES
DE PREFIJOS
En todos los ejemplos de este sitio y de la mayoría de los
casos reales se usan las unidades de medida del sistema internacional y sus
unidades derivadas. Sin embargo, muchas veces encontramos valores muy pequeños
o muy grandes por lo que se usan prefijos (tales como kilo, mili, micro, etc.).
Para hacer las cuentas necesitamos pasar todo a las unidades
base sin sus prefijos, pero haciendo esto probablemente obtengamos expresiones
y números muy largos con lo que es fácil cometer errores. Por ese motivo lo
recomendable es trabajar con una notación exponencial.
LOS PREFIJOS DE LAS UNIDADES:
NOTACIÓN CIENTÍFICA
La notación científica (o notación índice
estándar) es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder
expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un
producto:
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos
hispanohablantes.
CIFRAS SIGNIFICATIVAS
Las cifras significativas (o 'dígitos
significativos') representan el uso de una o más escala de incertidumbre en determinadas aproximaciones. Se dice que 2,7 tiene 2 cifras significativas, mientras que
2,70 tiene 3. Para distinguir los ceros que son significativos de los que no
son, estos últimos suelen indicarse como potencias de 10.
También cuando no se pueden poner más de tres cifras
simplemente se le agrega un número a el otro si es 5 o mayor que 5 y si es
menor simplemente se deja igual. Ejemplo 5,36789 solo se pueden mostrar tres
cifras así que se le suma un número a el 6 por que el 7 es mayor que 5 así que
queda 5,37 y si el número es menor que cinco así 5,36489 y se cortan queda 5,36
por que el 4 es menor que 5.
El uso de éstas considera que el último dígito de aproximación es incierto,
por ejemplo, al determinar el volumen de un líquido con una probeta cuya resolución es de 1 ml, implica una escala de incertidumbre
de 0,5 ml. Así se puede decir que el volumen de 6 ml será realmente
de 5,5 ml a 6,5 ml. El volumen anterior se representará entonces como
(6,0 ± 0,5) ml. En caso de determinar valores más próximos se tendrían que
utilizar otros instrumentos de mayor resolución, por ejemplo, una probeta de divisiones más finas y así
obtener (6,0 ± 0,1) ml o algo más satisfactorio según la resolución
requerida.
UNIDAD #2
REPRESENTACIÓN DE LOS VECTORES
1.
En función de su módulo y
ángulo: Está representado por las coordenadas (r; θ),
donde R es el módulo y θ es el ángulo
medido desde el eje positivo x hasta donde llega el vector. Llamadas también
coordenadas polares.
2.
Coordenadas rectangulares: Un
vector puede descomponerse en “x” y “y”, donde cada componente recibe el nombre
de coordenada rectangulares. Y en muchas veces se expresa en función de
los vectores base. “i” y “j”.
1.
Coordenadas geográficas: Está
definido por el par ordenado (r; rumbo), donde R representa el módulo del
vector, y rumbo la dirección del mismo, tomando en cuenta los puntos
cardinales.
2.
En función de su módulo y
unitario: Todo vector es igual al producto del módulo del mismo vector por
su unitario.
Ejemplos:
E=E. UE E=17 kgf (-0.598i +0.843j).
a. El vector E es igual al producto de
módulo por el unitario: E= (-9.15i+14.33j).
b.
En sus componentes rectangulares E=
-9.15i+14.33j.
c.
Para expresar en coordenadas
polares calculamos el ángulo:
cosα=
-0.518 α=122.55
→
θ=
122.55
cosβ=0.843→β=32.55 E=
(R;θ)
→(17kgf;
122.55).
d. Las coordenadas polares de un
vector determinan las coordenadas geográficas E= (17kgf; N 32.55º O).
MULTIPLICACIÓN
DE UN VECTOR POR UN ESCALAR
Se
llaman escalares a los números reales, cuando se está trabajando con vectores
en el plano cartesiano. Todo vector (a, b) se puede multiplicar por un escalar h, es decir por un número real h, de la siguiente manera: h(a, b)= (ha, hb).
Ejemplo:
Si
y
, entonces

OPERACIONES
CON VECTORES:
MÉTODO
DEL PARALELOGRAMO
Las cantidades
vectoriales no se suman tan simples como las escalares. Así por ejemplo, una
velocidad de 2 Km/h sumada con otra velocidad de 3 Km/h, no necesariamente da
como resultado 5 Km/h.
Para sumar vectores
se emplean diferentes métodos: el método del paralelogramo, el método
del triángulo, el método del polígono y el método de las
componentes rectangulares. A continuación trataremos el método del
paralelogramo.
Este método es una
alternativa al método del triángulo. En este método, se desplazan los vectores
para unir sus "colas". Luego se completa el paralelogramo y el vector
resultante será la diagonal trazada desde las "colas" de los vectores
a sumar. Este vector tendrá también la "cola" unida a las colas de
los otros dos y su "cabeza" estará al final de la diagonal. En la
figura 1se ilustra este método.
Ejemplo:
Los
vectores a y b de la figura 2 tienen magnitudes iguales a
6.0 y 7.0 unidades (u). Si forman un ángulo de 30º, calcular la magnitud y
dirección del vector resultante (vector suma) S.
Solución:
Para calcular la
resultante S podemos aplicar la ley de cosenos. Para ello
tengamos en cuenta que los ángulos
son suplementarios:



Para calcular la
dirección del vector resultante, basta con hallar el valor del ángulo
. Para lograr esto podemos utilizar la ley
de senos:



MÉTODO
DEL POLÍGONO
Cuando vamos a
sumar más de dos vectores, podemos sumar dos de ellos por el método del
triángulo. Luego el vector resultante sumarlo con otro vector también por el
método del triángulo, y así sucesivamente hasta llegar a obtener la resultante
final.
Otra forma de
hacer la suma, es utilizando el llamado método del polígono. Este método es
simplemente la extensión del método del triángulo. Es decir, se van desplazando
los vectores para colocarlos la "cabeza" del uno con la
"cola" del otro (un "trencito") y la resultante final es el
vector que cierra el polígono desde la "cola" que quedo libre hasta
la "cabeza" que quedo también libre (cerrar con un "choque de
cabezas"). Nuevamente el orden en que se realice la suma no interesa, pues
aunque el polígono resultante tiene forma diferente en cada caso, la resultante
final conserva su magnitud, su dirección y su sentido.
Este método sólo
es eficiente desde punto de vista gráfico, y no como un método analítico. En la
figura 1 se ilustra la suma de cuatro vectores.
Ejemplo. Sean los vectores:
Encontrar:
Resolviendo
por el método del polígono, la figura resultante es:
Si se utilizan los instrumentos de medición prácticos, se
obtiene que:
y que θ es aproximadamente 80ª.
Cuando dos vectores se restan, el
procedimiento anterior es el mismo, lo único que cambia es el sentido del
vector que le sigue al signo menos. Por ejemplo, al restar el vector D2 del
vector D1 se tiene:
D1- D2 = D1+ (-D2).
La expresión del miembro derecho de la ecuación anterior designa
un cambio en el sentido del vector D2; entonces, la expresión queda como una
suma, y por lo tanto, se sigue el procedimiento del método gráfico mostrado
anteriormente.
Los métodos gráficos ofrecen una manera sencilla de sumar o
restar dos o más vectores; pero cuando las magnitudes de los vectores son
demasiado grandes o poseen una gran cantidad de decimales, estos métodos se
vuelven imprecisos y difíciles de manipular a escalas de medición menores.
Es por eso, la necesidad de un método matemático nemotécnico,
que permita dar una mayor precisión en el cálculo de vectores resultantes, no
sólo en la magnitud, sino además en la dirección de ellas.
MÉTODO
ANALÍTICO DE LAS COMPONENTES
El método analítico se
basa en la descomposición de un vector como la suma de otros dos vectores,
llamados las componentes vectoriales del vector original. Ya habíamos hecho mención
de cómo obtener los componentes los componentes de un vector en algún post
anterior, y esta explicación nos ayudará para la suma de vectores por el método
analítico.
El método
analítico nos permite tener la certeza de que los resultados siempre son los correctos
ya que como no utilizamos herramientas físicas para la representación de los
vectores, como en los métodos gráficos, no corremos el riesgo de una mala
exactitud de los instrumentos y cualquier error que tenga que ver con ellos.
Otra ventaja del método analítico es que puede ser utilizado sobre un sistema
con un número ilimitado de vectores.
Procedimiento para
la solución por el método analítico:
VIDEO
En el video ya se
dan las componentes x, y de los vectores a sumar, por lo que resulta más fácil
y rápido aplicarlo, lo interesante sería que sólo dieran los vectores; para eso
tendríamos que obtener primero nosotros los componentes a través de las
funciones trigonométricas de seno y coseno. Una explicación mejor sobre este
última forma de solución la daré posteriormente.
PRODUCTO
PUNTO
El producto
punto o producto escalar de dos vectores es un número
real que resulta al multiplicar el producto de sus módulos por el
coseno del ángulo que forman.
Expresión
analítica del producto punto
Ejemplo:
Hallar el producto
punto de dos vectores cuyas coordenadas en una base ortonormal son: (1,
1/2, 3) y (4, −4, 1).
(1, 1/2, 3) ·
(4, −4,
1) = 1 ·
4 + (1/2) · (−4)
+ 3 ·
1 = 4 −2
+ 3 = 5
Expresión
analítica del módulo de un vector
Hallar el valor
del módulo de un vector de coordenadas
= (−3,
2, 5) en una base ortonormal.
Expresión
analítica del ángulo de dos vectores
Determinar
el ángulo que forman los vectores
= (1, 2, −3)
y
= (−2,
4, 1).
PRODUCTO
CRUZ
El producto
cruz o producto vectorial de dos vectores es otro vector cuya dirección es perpendicular a
los dos vectores y su sentido sería igual al avance de
un sacacorchos al girar de u a v. Su módulo es igual a:
El producto cruz se puede expresar mediante
un determinante:
Ejemplos:
Calcular el producto
cruz de los vectores
= (1, 2, 3) y
= (−1,
1, 2).
Dados los vectores

hallar el producto cruz de dichos
vectores. Comprobar que el vector hallado es ortogonal a

El producto
vectorial de
es ortogonal a los vectores  y
y  .
.